Understanding EM algorithm

本文主要内容为用一个简短的例子解释EM算法。

EM算法是聚类中常用的机器学习算法，但是相比喜闻乐见的k-means算法，大家可能对于EM算法的了解可能没有那么直观深入，所以本文主要利用一个简单的例子，在对比k-means算法的过程中，帮助大家建立一个清晰明确的对EM算法的理解。

当我们在聚类的领域谈论k-means算法时，分组的概念是非常清晰直观的–每个样本点只属于它离得最近的那个中心点所属的分组。如果给出一些样本点和中心，那么我们很容易给这些点打标签。

但是对于EM算法而言，分组的概念就么那么直观了（因为EM算法考虑每个样本点都有一定的概率属于所有的分组）。在我们介=引入EM算法之前，我们先复习一下k-means里面的分组概念。

k-means里面的分组概念

假设我们有如下的三个样本点（2D平面情况下的点）：

数据集 X Y
点0 10 5
点1 2 1
点2 3 7

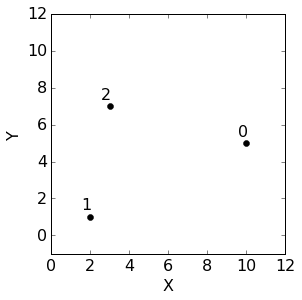
image

如果在上面的数据集上跑k-means算法，假定中心点如下：

中心 X Y
A 3 4
B 6 3
C 4 6

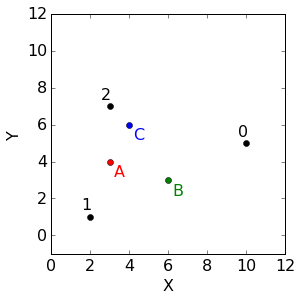
image

使用欧几里得距离，可以分配聚类如下

距离 群组A中心 群组B中心 群组C中心 群组分配
点0 7.071 4.472 6.083 群组B
点1 3.162 4.472 5.385 群组A
点2 3.000 5.000 1.414 群组C

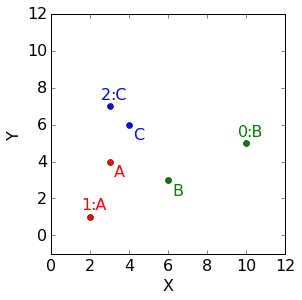
image

到此，我们可以给出一个回答：到底把一个点归类到一个群组意味着什么？举例来说，点1只被分配到分组A，也就是点1的100%属于群组A并且0%属于群组B和群组C。那么根据这个定义，我们可以得到如下表格，

群组A 群组B 群组C
点0 0 1 0
点1 1 0 0
点2 0 0 1
成员个数 1 1 1

注意到，对于一个群组来说，其得到的每一行的和都是1（因为一个点的百分比就是之和就是1）；另外，每一列的和就是这个群组的成员点的个数。推而广之：

  • 每一行的和总是1，因为一个点的百分比之和是1
  • 每一列的和就是分配到这个群组的点的个数

EM算法中的群组分配

到此为止，我们做的似乎不错，但是存在一个问题，我们这里每个点都只能属于一个群组，不过这一点有时候不是那么合理，比如点0分配到群组B似乎没什么问题，但是比如点1距离群组A和群组B的距离差别不那么大，那么只因为距离群组A近那么一点点就只把它分配到群组A，难道没什么问题吗？我们可能更加想表达这样一种概念：点1更可能属于群组A，但是我们也想保留点1也有一些可能属于群组B的不确定性。

距离 群组A中心 群组B中心 群组C中心 群组分配
点0 7.071 4.472 6.083 群组B
点1 3.162 4.472 5.385 群组A
点2 3.000 5.000 1.414 群组C

我们如何表述这种不确定性呢？这就是分组权重的由来。分组权重表达了一个点有多可能属于某个群组。比如之前的形式是这样的，

群组A 群组B 群组C
点0 0 1 0
点1 1 0 0
点2 0 0 1
成员个数 1 1 1

把上表的0和1换成分数（不要质疑这些分数怎么来的，等下会给出合理解释，：））

群组A 群组B 群组C
点0 0.007 0.938 0.055
点1 0.812 0.154 0.034
点2 0.234 0.016 0.750
软计数 1.053 1.108 0.839

上表中，点0以93.8%的概率属于群组B，同时下一行中，点1以81.2%的概率属于群组A。这些分数也就是分组权重。比如，点0属于分组A的权重就是0.7%。

和k-means算法中每个点只能属于一个群组不同，这里每个点都以某种程度地属于每一个群组。例如，93.8%的点0属于群组，其余的属于其他的群组。

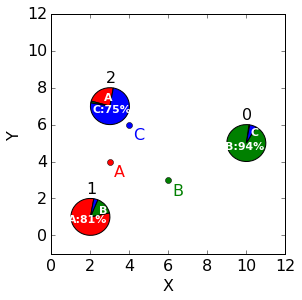
image

那么，在上面的分配矩阵里面，每一行和每一列的含义如下，

  • 每一行的和都是1，因为每个点都100%属于所有的群组，将这一些部分加起来和必定是1
  • 每一列的和是这个群组的“软计数”，它代表着所有的点属于这个群组的百分比之和
  • 所有的群组的软计数之和就是样本点的总数

步骤E：给定分组参数计算分组权重

分组权重是怎么来的？来自给定分组的分布的时候，我们观察样本点可能是什么。而EM算法中的每一个群组都由一个分组权重，一个均值向量，一个协方差矩阵构成。其中，均值表示群组的中心，协方差体现群组的范围，而分组权重体现了样本点与此分组的关联程度。所有，每个群组都由一个多变量高斯分布所定义。

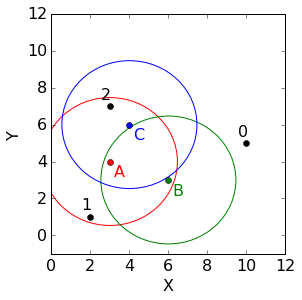
回顾上面的例子，加上一个不确定度的椭圆，如下，

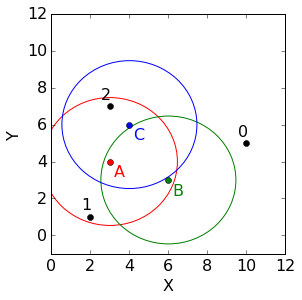
image

图中每个椭圆表示着协方差矩阵，在这个例子中，每个群组都是用的是对角协方差矩阵[[3,0],[0,3]]。因为对角线外元素都是0，所有图中的椭圆实际上看起来是圆。并且，由于并没有什么理由认为哪个群组比其他群组更加重要，那么我们定义每个群组的分组权重都是1/3。

那么，点0属于群组A的概率是多少？这里用来衡量潜在的高斯分布的标准是概率密度函数（probability density function，PDF），使用scipy.stats.multivariate_normal.pdf可计算出来：

1
2
print multivariate_normal.pdf([10,5], mean=[3,4], cov=[[3,0],[0,3]])
>>> 1.275199678019219e-05

我们还要将这个概率乘以分组权重才行，

1
2
print 1/3.*multivariate_normal.pdf([10,5], mean=[3,4], cov=[[3,0],[0,3]])
>>> 4.2506655934e-06

点0属于群组A的似然值是4.251e-6。单看看不出什么，我们还要依次计算群组B和群组C的值。分别计算B和C的PDF并且乘以分组权重：

1
2
print 1/3.*multivariate_normal.pdf([10,5], mean=[6,3], cov=[[3,0],[0,3]])
>>> 0.000630854709005
1
2
print 1/3.*multivariate_normal.pdf([10,5], mean=[4,6], cov=[[3,0],[0,3]])
>>> 3.71046481027e-05

那么，总结一下，

群组A 群组B 群组C
点(10,5)的PDF乘以分组权重 4.251e-6 6.309e-4 3.710e-5

很明显，群组B的似然值是最高的，这容易理解因为点0距离群组B中心的距离最近。

image

似然值看起来太小了，我么可以对其做一个归一化：都除以所有群组的似然值的和得到百分比值。

点0 群组A 群组B 群组C 总和
似然值 4.251e-6 6.309e-4 3.710e-5 6.722e-4
似然值，处以总和 4.251e-6 / 6.722e-4 = 0.007 6.309e-4 / 6.722e-4 = 0.938 3.710e-5 / 6.722e-4 = 0.055 -

最下一行就是点0分组责任！注意到因为归一化，这一行的总和是1。小结一下：

  • 对于每一个点我们计算了其高斯分布的PDF值，通过使用高斯分布的均值和协方差计算得到
  • 将PDF乘以分组权重，得到似然度
  • 将似然程度归一化

依次，我们可以得到点1和点2的矩阵，这里略去不表，最后将三个点的矩阵汇总得到以下，

Responsibility matrix Cluster A Cluster B Cluster C
Data point 0 0.007 0.938 0.055
Data point 1 0.812 0.154 0.034
Data point 2 0.234 0.016 0.750
Soft counts 1.053 1.108 0.839

步骤M：给定分组责任计算分组参数

现在我们手里已经有了分组的责任了，我们可以依据这些重新更新参数：分组权重、均值和协方差。虽然我们开始是乱猜的这些参数，但是通过更新我们可以得到一些更好的估计。

分组权重。群组的相对重要程度由它的软计数来决定。由于分组权重必须和为1，所有这里也需要做归一化，

| |Cluster A |Cluster B |Cluster C |Sum|
|-|-|-|-|
|Soft counts |1.053| 1.108| 0.839| 3.000|
|Soft counts, divided by the sum |1.053 / 3.000 = 0.351| 1.108 / 3.000 = 0.369 |0.839 / 3.000 = 0.280|-|

归一化后的软计数，就是分组权重的新的估计。

均值。使用分组责任计算所有点坐标的百分比，

1
2
3
4
5
6
7
8
[Weighted sum of data points for cluster A]
= [Fraction of data point 0 represented in cluster A] * [data point 0]
  + [Fraction of data point 1 represented in cluster A] * [data point 1]
  + [Fraction of data point 2 represented in cluster A] * [data point 2]
= 0.007*[data point 0] + 0.812*[data point 1] + 0.234*[data point 2]
= 0.007*(10,5) + 0.812*(2,1)  + 0.234*(3,7)
= (0.063,0.035) + (1.624,0.812) + (0.702,1.638)
= (2.396,2.485)

再除以软计数：

1
2
3
[mean of cluster A]
= (2.396,2.485)/1.053
= (2.275,2.360)

类似地计算B和C的均值，得到如下，

New means X Y
Cluster A 2.275 2.360
Cluster B 8.787 4.473
Cluster C 3.418 6.626

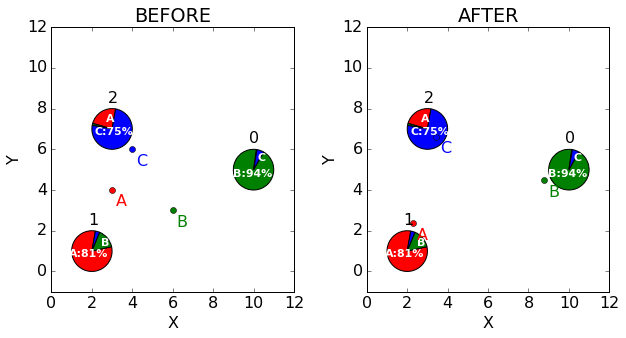
让我们画出均值的之前和之后的估计。注意到群组A的均值移动地更加靠近点1，因为群组A是主要的，类似的也发生在B和C上，

image

协方差。 协方差也是由分数来计算的，但是这里需要矩阵形式，所以实际上是由向量叉乘得到的，

$$x_i - \hat{\mu}_k$$

假设上面是d维向量，计算其与自身的内积，

$$(x_i - \hat{\mu}_k)(x_i - \hat{\mu}_k)^T$$

对012每个点都根据其坐标和A的均值计算协方差矩阵，与分组责任相乘：

1
2
3
4
5
6
7
8
9
10
11
12
13

[Weighted sum of outer products]
= [Fraction of data point 0 represented in cluster A] * [outer product for data point 0]
  + [Fraction of data point 1 represented in cluster A] * [outer product for data point 1]
  + [Fraction of data point 2 represented in cluster A] * [outer product for data point 2]
=  0.007*[[59.676,20.394], [20.394,6.970]]
  + 0.812*[[0.076,0.374], [0.374,1.850]]
  + 0.234*[[0.526,3.364], [3.364,21.530]]
= [[0.602, 1.234], [1.234, 6.589]]

[New covariance for cluster A]
= [[0.602,1.234], [1.234,6.589]]/1.053
= [[0.572,1.172], [1.172,6.257]]

对于BC重复以上，得到，

New covariances
Cluster A [[0.572,1.172], [1.172,6.257]]
Cluster B [[8.132,3.606], [3.606,2.004]]
Cluster C [[3.078,-0.518], [-0.518,1.581]]

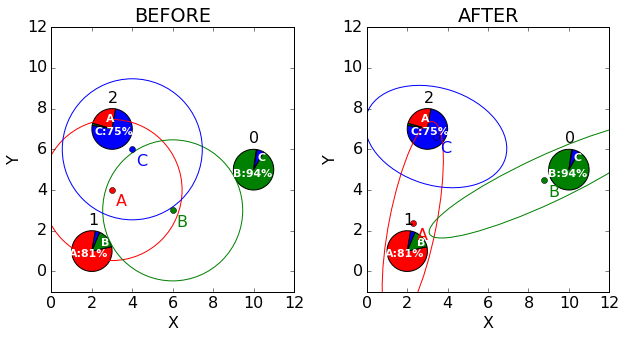
image

长于一口气！这么多的计算，我们到底更新的效果是什么？首先，所有的群组都有了更小的不确定度，从图上来看，椭圆变得更小了；其次，群组改变了形状来适应数据，比如群组B向着点1的方向延长了。总之，每次均值和协方差更新以后，群组都改变形状以更好地表示数据里的模式。

EM算法：交替步骤E和步骤M

现在我们对于分组的参数有了更好地估计，那么我们可以回过头去计算分组的责任，于是我们可以得到一个更好的参数的估计。实际上，我们可以交替着使用步骤E和步骤M来逐步提高分组的性能。

参考资料

  1. 华盛顿大学机器学习：聚类与检索