理解triplet loss


理解triplet loss，与给出TensorFlow和numpy两种形式的example code。

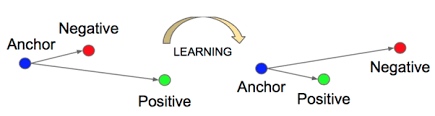
Triplet Loss 是当前应用的很广泛的一种损失函数，在人脸识别和聚类领域，这是一种很自然的映射与计算损失的方式，比如FaceNet里，通过构建一种embedding 方式，将人脸图像直接映射到欧式空间，而优化这种embedding的方法可以概括为，构建许多组三元组（Anchor，Positive，Negative），其中Anchor与Positive同label，Anchor与Negative不同label（在人脸识别里面，就是Anchor与Positive是同一个个体，而与Negative是不同个体），通过学习优化这个embedding，使得欧式空间内的Anchor与Positive 的距离比与Negative的距离要近。

公式表示

用公式表示就是，我们希望：

$$
\left\lVert f(x^a_i) - f(x^p_i) \right\rVert ^2_2 +
\alpha \lt \left\lVert f(x^a_i) - f(x^n_i) \right\rVert ^2_2 , \
\forall (f(x^a_i) , f(x^p_i) , f(x^n_i)) \in \mathscr T
$$

其中$\alpha$ 是强制的正例和负例之间的margin，$\mathscr T$是具有基数为$N$的训练集中的三元组的集合。

那么，损失函数很自然的可以写为：

$$
\sum^N_i
\Bigl [
\left\lVert f(x^a_i) - f(x^p_i) \right\rVert ^2_2 -
\left\lVert f(x^a_i) - f(x^n_i) \right\rVert ^2_2 + \alpha
\Bigr ] _ +
$$

其中加号指的，如果中括号内部分小于0，则没有损失（Anchor与Positive的距离加上margin小于与Negative的距离），否则计算这个距离为损失。

代码表示

Numpy 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import numpy as np

batch_size = 3*12
embedding_size = 16

# 构造batch_size * embedding_size 维度的随机矩阵
emb = np.random.uniform(size=[])

# 对emb逢三取1、2、3行分别为Anchor、Positive、Negative
# 计算其2范数的距离即欧氏距离
pos_dist_sqr = np.sum(np.square(emb[0::3,:]-emb[1::3,:]), axis=1)        
neg_dist_sqr = np.sum(np.square(emb[0::3,:]-emb[2::3,:]), axis=1)

# 这里就是照抄公式了，注意mean和sum是一样的
np_triplet_loss = np.mean(np.maximum(0., pos_dist_sqr-neg_dist_sqr+alpha))

TensorFlow 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import tensorflow as tf

batch_size = 3*12
embedding_size = 16
alpha = 0.2

def triplet_loss(anchor, positive, negative, alpha):   
    with tf.variable_scope('triplet_loss'):
        pos_dist = tf.reduce_sum(tf.square(tf.subtract(anchor, positive)), 1)
        neg_dist = tf.reduce_sum(tf.square(tf.subtract(anchor, negative)), 1)
        basic_loss = tf.add(tf.subtract(pos_dist, neg_dist), alpha)
        loss = tf.reduce_mean(tf.maximum(basic_loss, 0.0), None)
    return loss

# 构建矩阵
embeddings = tf.placeholder(np.float64, shape=(batch_size, embedding_size), name='embeddings')
# 先将embeddings矩阵第0维resize为(?, 3)维，第1维不变，变为三维矩阵(-1, 3, embedding_size)，再在其第二维度为3上unstack为三份
anchor, positive, negative = tf.unstack(tf.reshape(embeddings, shape=(-1, 3, embedding_size)), axis=1)

完整代码如下，这里测试对比了两种实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import tensorflow as tf
import numpy as np

batch_size = 3*12
embedding_size = 16
alpha = 0.2

def triplet_loss(anchor, positive, negative, alpha):   
    with tf.variable_scope('triplet_loss'):
        pos_dist = tf.reduce_sum(tf.square(tf.subtract(anchor, positive)), 1)
        neg_dist = tf.reduce_sum(tf.square(tf.subtract(anchor, negative)), 1)
        basic_loss = tf.add(tf.subtract(pos_dist, neg_dist), alpha)
        loss = tf.reduce_mean(tf.maximum(basic_loss, 0.0), None)
    return loss

with tf.Graph().as_default():
    embeddings = tf.placeholder(np.float64, shape=(batch_size, embedding_size), name='embeddings')
    anchor, positive, negative = tf.unstack(tf.reshape(embeddings, shape=(-1, 3, embedding_size)), axis=1)
    triplet_loss = triplet_loss(anchor, positive, negative, alpha)
    
    sess = tf.Session()
    with sess.as_default():
        np.random.seed(666)
        emb = np.random.uniform(size=[batch_size, embedding_size])
        tf_triplet_loss = sess.run(triplet_loss, feed_dict={embeddings:emb})
        
        pos_dist_sqr = np.sum(np.square(emb[0::3,:]-emb[1::3,:]), axis=1)        
        neg_dist_sqr = np.sum(np.square(emb[0::3,:]-emb[2::3,:]), axis=1)
        np_triplet_loss = np.mean(np.maximum(0., pos_dist_sqr-neg_dist_sqr+alpha))
        
        np.testing.assert_almost_equal(tf_triplet_loss, np_triplet_loss, decimal=5, err_msg='Triplet loss is incorrect')