Google Rephil是Google AdSense背后广告相关性计算的头号秘密武器。但是这个系统没有发表过论文。只是其作者(博士Uri Lerner和工程师Mike Yar)在2002年在湾区举办的几次小规模交流中简要介绍过。所以Kevin Murphy把这些内容写进了他的书《Machine Learning: a Probabilitic Perspecitve》里。在吴军博士的《数学之美》里也提到了Rephil。
Rephil的模型是一个全新的模型,更像一个神经元网络。这个网络的学习过程从Web scale的文本数据中归纳海量的语义——比如“apple”这个词有多个意思:一个公司的名字、一种水果、以及其他。当一个网页里包含”apple”, “stock”, “ipad”等词汇的时候,Rephil可以告诉我们这个网页是关于apple这个公司的,而不是水果。
这个功能按说pLSA和LDA也都能实现。为什么需要一个全新的模型呢? 从2007年至今,国内外很多团队都尝试过并行化pLSA和LDA。心灵手巧的工程师们,成功的开发出能学习数万甚至上十万语义(latent topics)的训练系统。但是不管大家用什么训练数据,都会发现,得到的大部分语义(相关的词的聚类)都是非常类似,或者说“重复”的。如果做一个“去重”处理,几万甚至十万的语义,就只剩下几百几千了。
这是怎么回事?
如果大家尝试着把训练语料中的低频词去掉,会发现训练得到的语义和用全量数据训练得到的差不多。换句话说,pLSA和LDA模型的训练算法没有在意低频数据。
为什么会这样呢?因为pLSA和LDA这类概率模型的主要构造单元都是指数族分布(exponential family)。比如pLSA假设一个文档中的语义的分布是multinomial的,每个语义中的词的分布也是multinomial的。因为multinomial是一种典型的指数族分布,这样整个模型描述的海量数据的分布,不管哪个维度上的marginalization,都是指数族分布。在LDA中也类似——因为LDA假设各个文档中的语义分布的multinomial distributions的参数是符合Dirichlet分布的,并且各个语义中的词的分布的multinomial distributions的参数也是符合Dirichlet分布的,这样整个模型是假设数据是指数族分布的。
可是Internet上的实际数据基本都不是指数族分布的——而是长尾分布的。至于为什么是这样?可以参见2006年纽约时报排名畅销书The Long Tail: Why the Future of Business is Selling Less of More。或者看看其作者Chris Anderson的博客The Long Tail。
长尾分布的形状大致如下图所示:
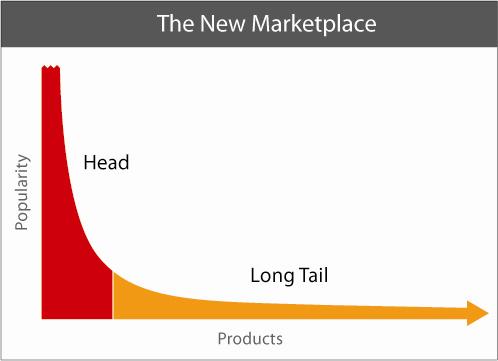
其中x轴表示数据的类型,y轴是各种类型的频率,少数类型的频率很高(称为大头,图中红色部分),大部分很低,但是大于0(称为长尾,图中黄色部分)。一个典型的例子是文章中词的分布,有个具体的名字Zipf’s law,就是典型的长尾分布。而指数族分布基本就只有大头部分——换句话说,如果我们假设长尾数据是指数族分布的,我们实际上就把尾巴给割掉了。
割掉数据的尾巴——这就是pLSA和LDA这样的模型做的——那条长尾巴覆盖的多种多样的数据类型,就是Internet上的人生百态。理解这样的百态是很重要的。比如百度和Google为什么能如此赚钱?因为互联网广告收益。传统广告行业,只有有钱的大企业才有财力联系广告代理公司,一帮西装革履的高富帅聚在一起讨论,竞争电视或者纸媒体上的广告机会。互联网广告里,任何人都可以登录到一个网站上去投放广告,即使每日广告预算只有几十块人民币。这样一来,刘备这样织席贩屡的小业主,也能推销自己做的席子和鞋子。而搜索引擎用户的兴趣也是百花齐放的——从人人爱戴的陈老师苍老师到各种小众需求包括“红酒木瓜汤”(一种丰胸秘方,应该出丰胸广告)或者“苹果大尺度”(在搜索范冰冰主演的《苹果》电影呢)。把各种需求和各种广告通过智能技术匹配起来,就酝酿了互联网广告的革命性力量。这其中,理解各种小众需求、长尾意图就非常重要了。
实际上,Rephil就是这样一个能理解百态的模型。因为它把Google AdSense的盈利能力大幅提升,最终达到Google收入的一半。两位作者荣获Google的多次大奖,包括Founders’ Award。
而切掉长尾是一个很糟糕的做法。大家还记得小说《1984》里有这样一个情节吗?老大哥要求发布“新话”——一种新的语言,删掉自然英语中大部分词汇,只留下那些主流的词汇。看看小说里的人们生活的世界,让人浑身发毛,咱们就能体会“割尾巴”的恶果了。没有看过《1984》的朋友可以想象一下水木首页上只有“全站十大”,连“分类十大”都删掉之后的样子。
既然如此,为什么这类模型还要假设数据是指数族分布的呢?——实在是不得已。指数族分布是一种数值计算上非常方便的数学元素。拿LDA来说,它利用了Dirichlet和multinomial两种分布的共轭性,使得其计算过程中,模型的参数都被积分给积掉了(integrated out)。这是AD-LDA这样的ad hoc并行算法——在其他模型上都不好使的做法——在LDA上好用的原因之一。换句话说,这是为了计算方便,掩耳盗铃地假设数据是指数族分布的。
实际上,这种掩耳盗铃在机器学习领域很普遍。比如有个兄弟听了上面的故事后说:“那我们就别用概率模型做语义分析了,咱们还用矩阵分解吧?SVD分解怎么样?” 很不好意思的,当我们把SVD分解用在语义分析(称为LSA,latent semantic analysis)上的时候,我们还是引入了指数族分布假设——Gaussian assumption或者叫normality assumption。这怎么可能呢?SVD不就是个矩阵分解方法吗?确实传统SVD没有对数据分布的假设,但是当我们用EM之类的算法解决存在missing data的问题——比如LSA,还有推荐系统里的协同过滤(collaborative filtering)——这时不仅引入了Gaussian assumption,而且引入了linearity assumption。当我们用其他很多矩阵分解方法做,都存在同样的问题。
掩耳盗铃的做法怎么能存在得如此自然呢?这是因为指数族分布假设(尤其是Gaussian assumption)有过很多成功的应用,包括通信、数据压缩、制导系统等。这些应用里,我们关注的就是数据中的低频部分;而高频部分(或者说距离mean比较远的数据)即使丢掉了,电话里的声音也能听懂,压缩还原的图像也看得明白,导弹也还是能沿着“最可能”靠谱的路线飞行。我们当然会假设数据是指数族分布的,这样不仅省计算开销,而且自然的忽略高频数据,我们还鄙夷地称之为outlier或者noise。
可是在互联网的世界里,正是这些五花八门的outliers和noise,蕴含了世间百态,让数据不可压缩,从而产生了“大数据”这么个概念。处理好大数据的公司,赚得盆满钵满,塑造了一个个传奇。这里有一个听起来比较极端的说法大数据里无噪声——很多一开始频率很低,相当长尾,会被词过滤系统认为是拼写错误的queries,都能后来居上成为主流。比如“神马”,“酱紫”。
Rephil系统实现的模型是一个神经元网络模型(neural network)。它的设计的主要考虑,就是要能尽量好的描述长尾分布的文本数据和其中蕴含的语义。Rephil模型的具体技术细节因为没有在论文中发表过,所以不便在这里透露。但是Rephil模型描述长尾数据的能力,是下文将要介绍的Peacock系统的原动力,虽然两者在模型上完全不同。
Rephil系统是基于Google MapReduce构建的。如上节所述,MapReduce在用来实现迭代算法的时候,效率是比较低的。这也是Peacock要设计全新框架的原动力——使其比MapReduce高效,但同时像MapReduce一样支持fault recovery。