精确率、召回率、F1 值、ROC、AUC、PRC都是机器学习模型的常用评价标准,那么它们的区别和联系以及各自应用场景是什么呢?
这些指标的含义
1 | Precision:P=TP/(TP+FP) |
TP —— True Positive (真正, TP)被模型预测为正的正样本;可以称作判断为真的正确率
TN —— True Negative(真负 , TN)被模型预测为负的负样本 ;可以称作判断为假的正确率
FP ——False Positive (假正, FP)被模型预测为正的负样本;可以称作误报率
FN—— False Negative(假负 , FN)被模型预测为负的正样本;可以称作漏报率
True Positive Rate(真正率 , TPR)或灵敏度(sensitivity) 也就是召回率 Recall
TPR = TP /(TP + FN)
正样本预测结果数 / 正样本实际数
True Negative Rate(真负率 , TNR)或特指度(specificity)
TNR = TN /(TN + FP)
负样本预测结果数 / 负样本实际数
False Positive Rate (假正率, FPR)
FPR = FP /(FP + TN)
被预测为正的负样本结果数 /负样本实际数
False Negative Rate(假负率 , FNR)
FNR = FN /(TP + FN)
被预测为负的正样本结果数 / 正样本实际数
假定一个具体场景作为例子:
假如某个班级有男生80人,女生20人,共计100人.目标是找出所有女生.
现在某人挑选出50个人,其中20人是女生,另外还错误的把30个男生也当作女生挑选出来了.
作为评估者的你需要来评估(evaluation)下他的工作。
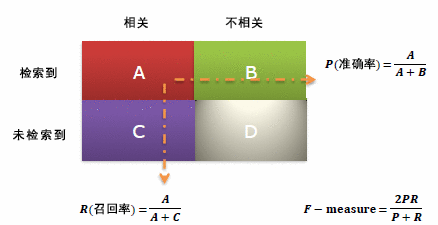
| 相关(Relevant),正类 | 无关(NonRelevant),负类 | |
|---|---|---|
| 被检索到(Retrieved) | true positives(TP 正类判定为正类,例子中就是正确的判定”这位是女生”) | false positives(FP 负类判定为正类,”存伪”,例子中就是分明是男生却判断为女生,当下伪娘横行,这个错常有人犯) |
| 未被检索到(Not Retrieved) | false negatives(FN 正类判定为负类,”去真”,例子中就是,分明是女生,这哥们却判断为男生–梁山伯同学犯的错就是这个) | true negatives(TN 负类判定为负类,也就是一个男生被判断为男生,像我这样的纯爷们一准儿就会在此处) |
通过这张表,我们可以很容易得到这几个值:
TP=20
FP=30
FN=0
TN=50
**精确率: **策略命中的所有相关样本/策略命中的所有样本
Precision = TP / (TP + FP)
注:正确率/准确率(accuracy)和 精度(precision)不是一个概念
正确率是我们最常见的评价指标,accuracy = (TP+TN)/(P+N),这个很容易理解,就是被分对的样本数除以所有的样本数
召回率:策略命中的所有相关样本/所有的相关样本(包括策略未被命中的)
Recall = TP / (TP + FN)
F1-score(F1-分数):2×准确率×召回率/(准确率+召回率),是模型准确率和召回率的一种加权平均,它的最大值是1,最小值是0。(详细介绍见下)
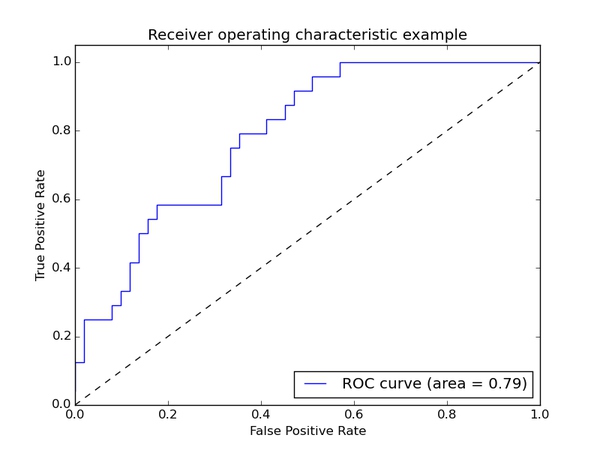
ROC(_receiver operating characteristic curve_): ROC曲线的横坐标为_false positive rate_(FPR,假正率),纵坐标为_true positive rate_(TPR,真正率,召回率)
PRC(_precision recall curve_): PRC曲线的横坐标为召回率_Recall_,纵坐标为准确率_Precision_。
AUC:被定义为ROC曲线下的面积,显然这个面积的数值不会大于1。故AUC与PRC是同一概念。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围一般在0.5和1之间。
指标的评价标准
ROC与AUC
ROC(receiver operating characteristic curve)也就是下图中的曲线,其关注两个指标
True Positive Rate ( TPR ) = TP / [ TP + FN] ,TPR代表能将正例分对的概率
False Positive Rate( FPR ) = FP / [ FP + TN] ,FPR代表将负例错分为正例的概率
在ROC 空间中,每个点的横坐标是FPR,纵坐标是TPR,这也就描绘了分类器在TP(真正的正例)和FP(错误的正例)间的trade-off。ROC的主要分析工具是一个画在ROC空间的曲线——ROC curve。我们知道,对于二值分类问题,实例的值往往是连续值,我们通过设定一个阈值,将实例分类到正类或者负类(比如大于阈值划分为正类)。因此我们可以变化阈值,根据不同的阈值进行分类,根据分类结果计算得到ROC空间中相应的点,连接这些点就形成ROC curve。ROC curve经过(0,0)(1,1),实际上(0, 0)和(1, 1)连线形成的ROC curve实际上代表的是一个随机分类器。一般情况下,这个曲线都应该处于(0, 0)和(1, 1)连线的上方。如图所示。
用ROC curve来表示分类器的performance很直观好用。可是,人们总是希望能有一个数值来标志分类器的好坏。
于是**Area Under roc Curve(AUC)**就出现了。顾名思义,AUC的值就是处于ROC curve下方的那部分面积的大小。通常,AUC的值介于0.5到1.0之间,较大的AUC代表了较好的Performance。
同时我们也看里面也上了AUC也就是是面积。一般来说,如果ROC是光滑的,那么基本可以判断没有太大的overfitting(比如图中0.2到0.4可能就有问题,但是样本太少了),这个时候调模型可以只看AUC,面积越大一般认为模型越好。
PRC
再说PRC, precision recall curve。和ROC一样,先看平滑不平滑(蓝线明显好些),在看谁上谁下(同一测试集上),一般来说,上面的比下面的好(绿线比红线好)。F1(下面介绍)当P和R接近就也越大,一般会画连接(0,0)和(1,1)的线,线和PRC重合的地方的F1是这条线最大的F1(光滑的情况下),此时的F1对于PRC就好象AUC对于ROC一样。一个数字比一条线更方便调模型。
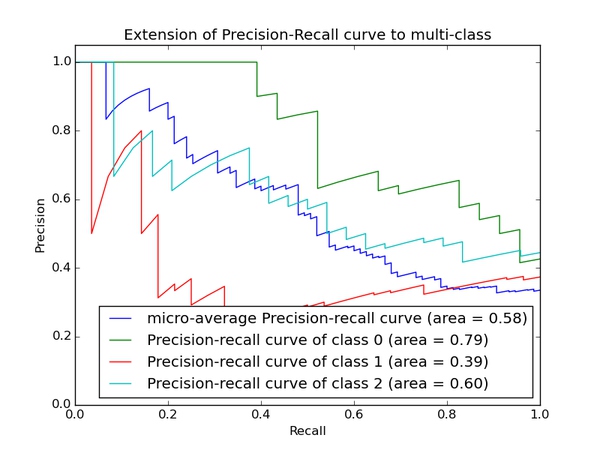
以上两个指标用来判断模型好坏,但是有时候模型没有单纯的谁比谁好(比如图二的蓝线和青线),那么选择模型还是要结合具体的使用场景。
下面是两个场景:
- 地震的预测
对于地震的预测,我们希望的是RECALL非常高,也就是说每次地震我们都希望预测出来。这个时候我们可以牺牲PRECISION。情愿发出1000次警报,把10次地震都预测正确了;也不要预测100次对了8次漏了两次。
- 嫌疑人定罪
基于不错怪一个好人的原则,对于嫌疑人的定罪我们希望是非常准确的。及时有时候放过了一些罪犯(recall低),但也是值得的。
对于分类器来说,本质上是给一个概率,此时,我们再选择一个CUTOFF点(阀值),高于这个点的判正,低于的判负。那么这个点的选择就需要结合你的具体场景去选择。反过来,场景会决定训练模型时的标准,比如第一个场景中,我们就只看RECALL=99.9999%(地震全中)时的PRECISION,其他指标就变得没有了意义。
PRC比ROC更有效的特殊情况
在正负样本分布得极不均匀(highly skewed datasets)的情况下,PRC比ROC能更有效地反应分类器的好坏。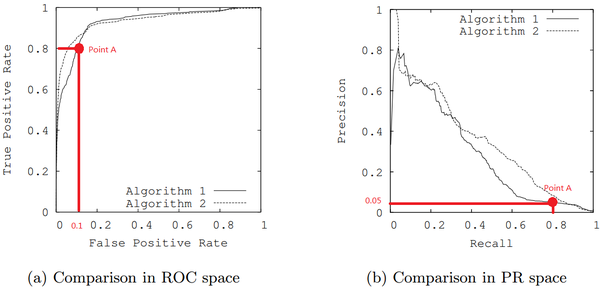
例如上图中图(a)ROC曲线中的两个模型看似非常接近左上角,但是对应着同一点的图(b)中的PRC曲线中我们可以发现,在召回率为0.8时准确率只有0.05之少,这是由于正负样本比例失衡造成的。
再如下图:
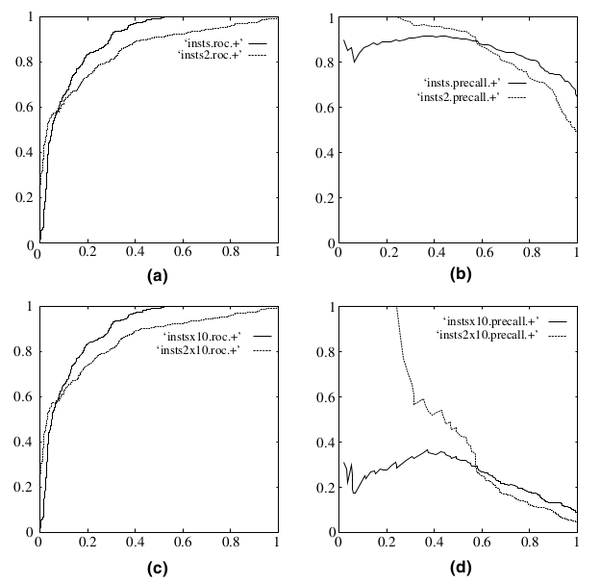
在testing set出现imbalance时ROC曲线能保持不变,而PR则会出现大变化。引用图(Fawcett, 2006),(a)(c)为ROC,(b)(d)为PR,(a)(b)样本比例1:1,(c)(d)为1:10。
F1
信息检索、分类、识别、翻译等领域两个最基本指标是**召回率(Recall Rate)和准确率(Precision Rate)**,召回率也叫查全率,准确率也叫查准率。
图表表示如下:
准确率和召回率是互相影响的,理想情况下肯定是做到两者都高,但是一般情况下准确率高、召回率就低,召回率低、准确率高,当然如果两者都低,那是什么地方出问题了。一般情况,用不同的阀值,统计出一组不同阀值下的精确率和召回率,这就是PRC曲线。如下图:
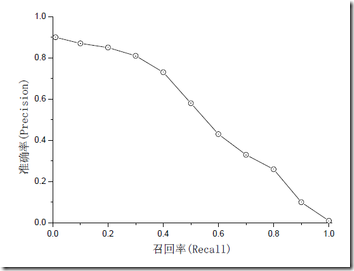
如果是做搜索,那就是保证召回的情况下提升准确率;如果做疾病监测、反垃圾,则是保准确率的条件下,提升召回。
所以,在两者都要求高的情况下,可以用F1来衡量。
F1 = 2 * P * R / (P + R)
总结
- AUC是ROC的积分(曲线下面积),是一个数值,一般认为越大越好,数值相对于曲线而言更容易当做调参的参照。
- ROC相比PRC在正负样本比例悬殊时具有保持单调性的特性,学术论文在假定正负样本均衡的时候多用ROC/AUC。
- 实际工程更多存在数据标签倾斜问题一般使用F1。