神经网络术语大百科：优化函数、激活函数、损失函数、正则方法的简介

简述关于神经网络的各种优化函数（SGD，Adagrad，Adadelta，Adam，Adamax，Nadam）、各种激活函数（Sigmoid，Tanh、Hard Sigmoid、Softplus、ReLU、ElU、PReLU、RReLU）、各种损失函数以及正则方法的简述，并附带代码实现例子。

优化函数

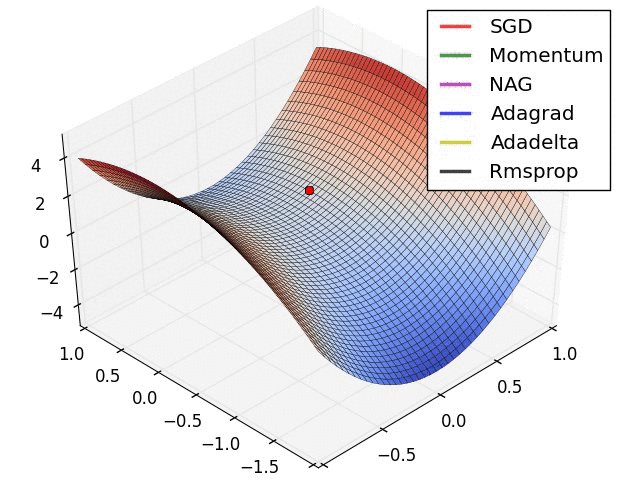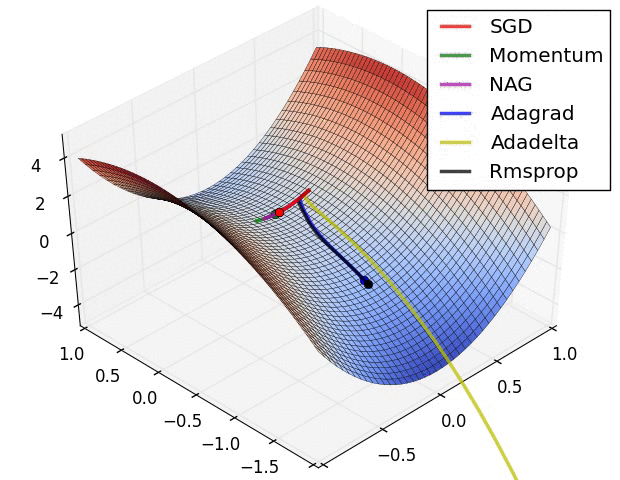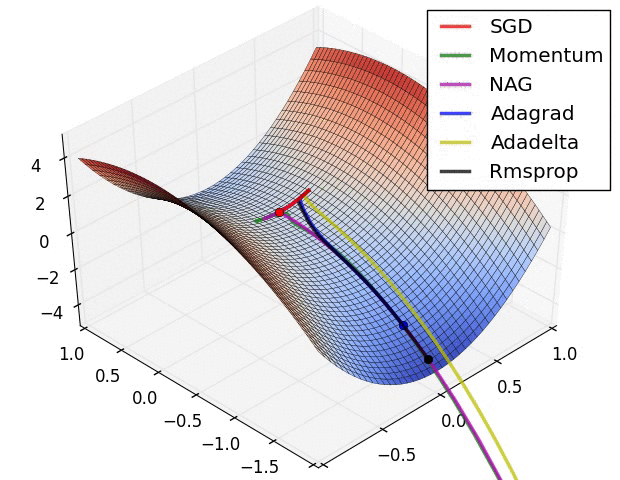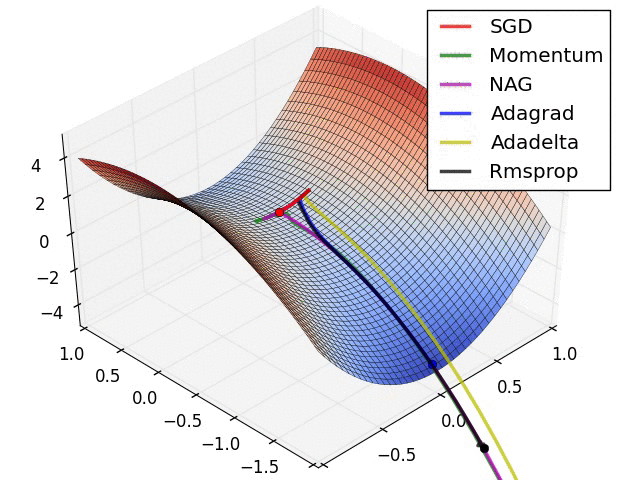
先上两张图

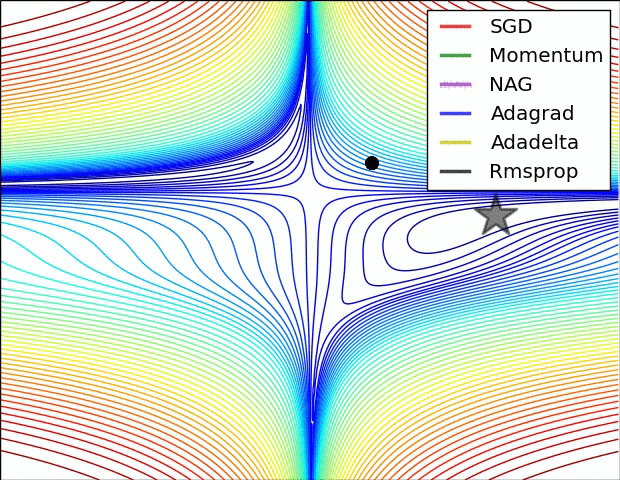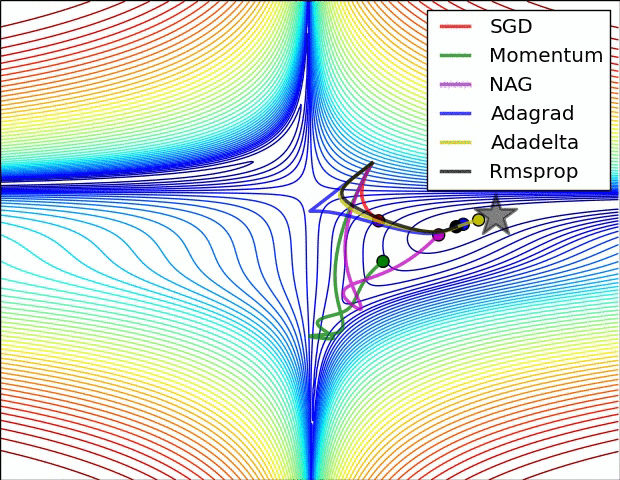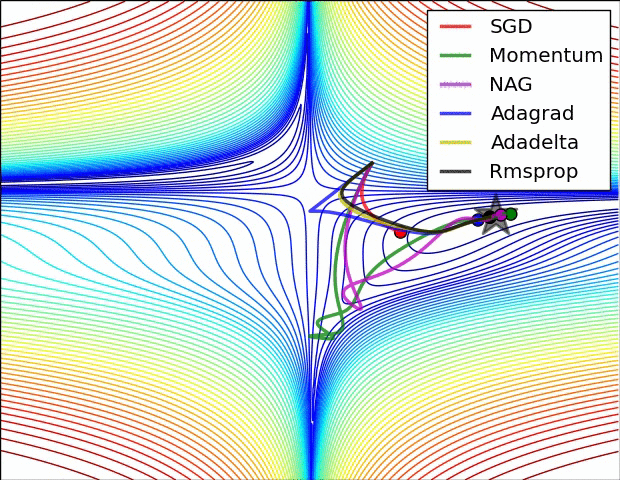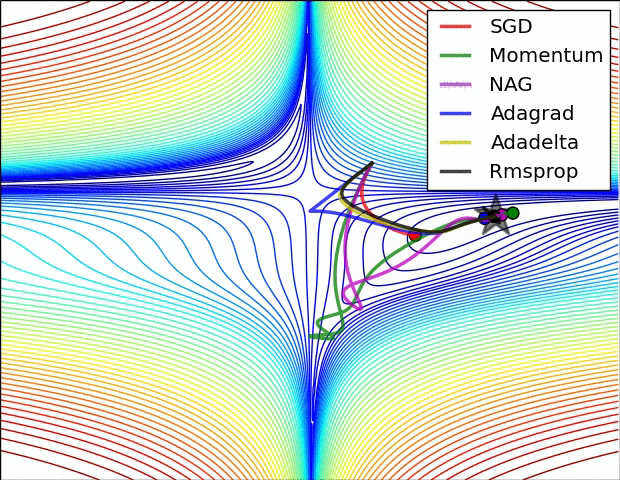
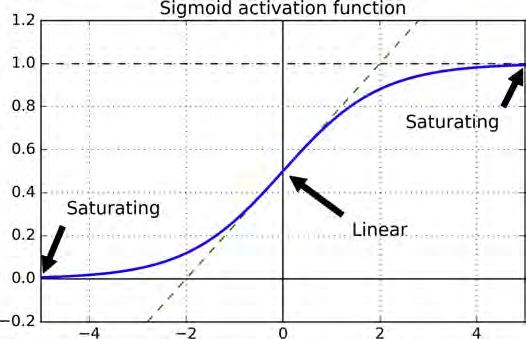
激活函数

没有激活函数，神经元就只是一个线性函数，那么无论多少层的神经元叠加是没有意义的。而主流激活函数也随着神经网络、深度学习的发展迭代进化了许多次代。

Sigmoid

Sigmoid是S形状的意思，又因为它是逻辑回归的激活函数又叫logistic函数，函数式为$y = 1 / (1 + exp(-x))$是很早以前最常用的激活函数，其实也是有一些优点的，比如，

• 值域位于0-1，那么对于逻辑回归，这是对于二分类的一个很自然的表达，也就是概率
• 处处连续可导

不过呢，我们观察它的形状，可以得出，Sigmoid函数在两端（靠近0和1的部分）梯度很小，这也意味着，如果神经元的输出落到了这个地方，那么它几乎没什么梯度可以传到后面，而随着神经网络的层层削弱，后面的层（靠近输入的层）没有多少梯度能传过来，几乎就“学不到什么”了。这叫做梯度消失问题，一度是阻碍神经网络往更深的层进化的主要困难，导致深度学习专家们绞尽脑汁想了许多方法来对抗这个问题，比如“Xavier and He Initialization”，比如我们要把weight随机初始化为如下的范围，

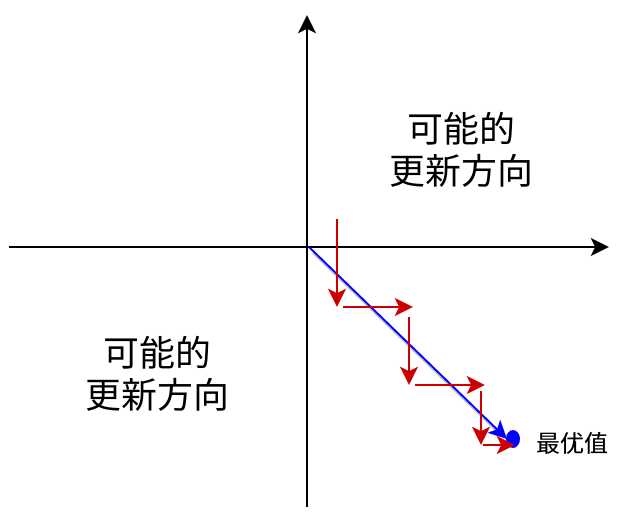
sigmoid的另一个问题是它不是0均值的，Sigmoid函数的输出值恒大于0，这会导致模型训练的收敛速度变慢。举例来讲，对，如果所有均为正数或负数，那么其对的导数总是正数或负数，这会导致如下图红色箭头所示的阶梯式更新，这显然并非一个好的优化路径。深度学习往往需要大量时间来处理大量数据，模型的收敛速度是尤为重要的。所以，总体上来讲，训练深度学习网络尽量使用zero-centered数据 (可以经过数据预处理实现) 和zero-centered输出。

如今，sigmoid函数应用最广泛的在于其变种softmax在多元分类中，比如手写数字识别，经过卷积神经网络的处理，最后我们需要网络输出每个预测的概率值，最后预测为某一个数字，这里就需要用到softmax，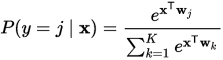

以下是softmax的Keras代码，注意其中一个trick，e = K.exp(x - K.max(x, axis=axis, keepdims=True))这里每个分量减去最大值是为了减少计算量。

def softmax(x, axis=-1):
    """Softmax activation function.

    # Arguments
        x : Tensor.
        axis: Integer, axis along which the softmax normalization is applied.

    # Returns
        Tensor, output of softmax transformation.

    # Raises
        ValueError: In case `dim(x) == 1`.
    """
    ndim = K.ndim(x)
    if ndim == 2:
        return K.softmax(x)
    elif ndim > 2:
        e = K.exp(x - K.max(x, axis=axis, keepdims=True))
        s = K.sum(e, axis=axis, keepdims=True)
        return e / s
    else:
        raise ValueError('Cannot apply softmax to a tensor that is 1D')

tanh

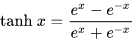
tanh 是sigmoid的变形： $tanh(x)=2sigmoid(2x)-1$，与 sigmoid 不同的是，tanh 是0均值的。因此，实际应用中，tanh 会比 sigmoid 更好一些，

ReLU家族

然而标准ReLU不是完美的，比如因为ReLU在小于0的坐标梯度都是0，那么会造成“死亡”的神经元的问题：一旦神经元的输入与权重之乘积是负的，那么经过ReLU的激活，输出就是0，而ReLU的0梯度让“死亡”的神经元无法“复活”：没办法回到输出不是0的状态，这样就出现了许多在ReLU的变种，一般都是对标准ReLU坐标轴左边的部分做文章，比如leaky ReLU。其公式就是$LeakyReLU_ α (z) = max(\alpha z,z)$。如图，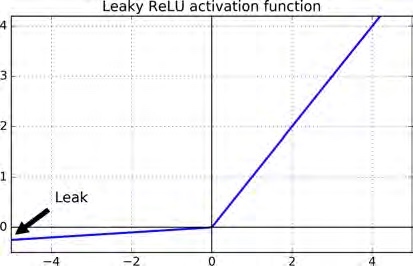

这篇文章Empirical Evaluation of Rectified Activations in Convolution Network对比了几种leaky ReLU，比如把$\alpha$设置为0.2效果总是好过0.01，并且，对于randomized leaky ReLU (RReLU)（其中$\alpha$设置为一个在指定范围内的随机数），效果也不错，而且还具有一定的正则作用。另外，对于parametric leaky ReLU (PReLU)（其中$\alpha$作为网络的一个参数，被反向传播学习出来，之前的$\alpha$都是超参数，不能学只能调节），这种变种对于大数据集不错，但是数据量过小就有过拟合的风险。以下是Keras里面relu的代码，

def relu(x, alpha=0., max_value=None):
    """Rectified linear unit.

    With default values, it returns element-wise `max(x, 0)`.

    # Arguments
        x: A tensor or variable.
        alpha: A scalar, slope of negative section (default=`0.`).
        max_value: Saturation threshold.

    # Returns
        A tensor.
    """
    if alpha != 0.:
        negative_part = tf.nn.relu(-x)
    x = tf.nn.relu(x)
    if max_value is not None:
        max_value = _to_tensor(max_value, x.dtype.base_dtype)
        zero = _to_tensor(0., x.dtype.base_dtype)
        x = tf.clip_by_value(x, zero, max_value)
    if alpha != 0.:
        alpha = _to_tensor(alpha, x.dtype.base_dtype)
        x -= alpha * negative_part
    return x

另外，在这篇文章里面FAST AND ACCURATE DEEP NETWORK LEARNING BY EXPONENTIAL LINEAR UNITS (ELUS)，引入了一种新的ReLU，exponential linear unit (ELU)，公式如下，
$$
ELU_{\alpha}(z) = \alpha (\exp(z)-1) \ if \ z \lt 0 ; \ z \ if \ z \gt 0;
$$

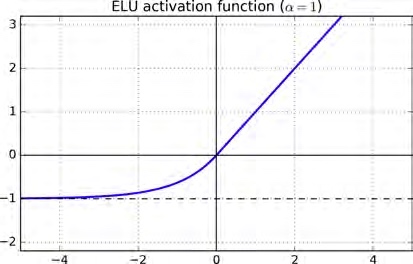
与标准ReLU最大的区别在于它处处连续可导，这使得梯度下降得到加速，收敛得到了加速，而使用了指数函数使得其测试阶段的计算代价更高。Keras里elu的实现，

def elu(x, alpha=1.):
    """Exponential linear unit.

    # Arguments
        x: A tenor or variable to compute the activation function for.
        alpha: A scalar, slope of positive section.

    # Returns
        A tensor.
    """
    res = tf.nn.elu(x)
    if alpha == 1:
        return res
    else:
        return tf.where(x > 0, res, alpha * res)

激活函数的选择

一般来说，我们的选择顺序可以理解为：
ELU > leaky ReLU (以及其变种) > ReLU > tanh > logistic。但是，

• 如果我们更顾虑模型运行速度，那么leaky ReLU可能比ELU更好；
• 如果我们不想调节超参数，那么用默认的$\alpha$就行，ReLU和ELU的分别是0.01和1；
• 如果算力足够可以用来调参，那么如果网络过拟合我们会选择RReLU，如果训练集数据足够多，那可以用PReLU。