卷积神经网络(Convolutional Neural Network),简称CNN,是机器视觉领域的主要神经网络模型。本文主要对CNN做一个简明全面的介绍。
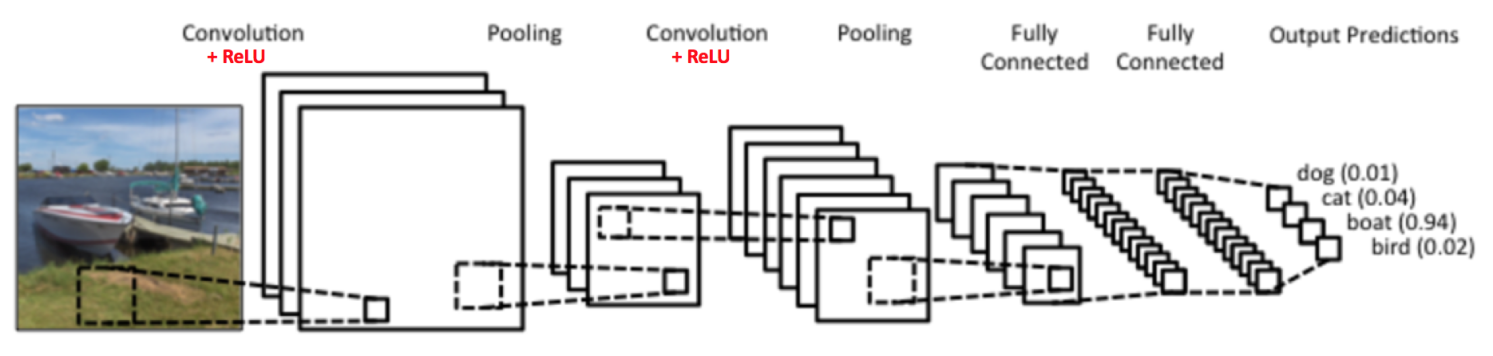
上图是90年代的LeNet的结构,当时主要用于字符的识别,当前有许多的新的CNN结构,但是大体上都是采用了与LeNet类似的主要思想。本文主要以LeNet为例来做讲解。
LeNet的主要组成部分:
- 卷积层
- 非线性变换(ReLU)
- 池化层或者下采样
- 分类(全连接)
图片就是矩阵
在讲卷积与卷积层之前,我们首先介绍一下图片的相关的概念。本质上,每张图片都是像素值的矩阵。
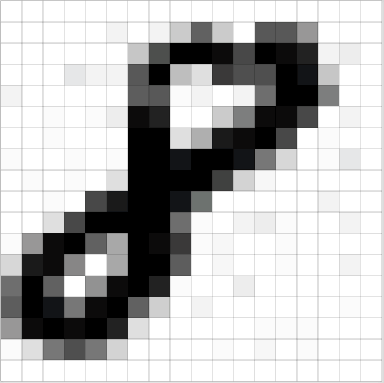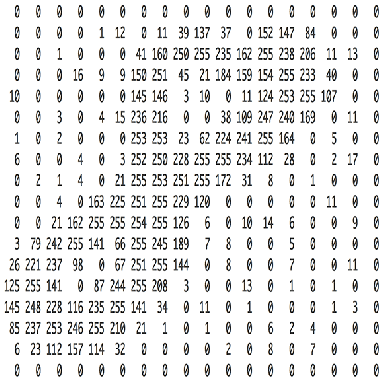
彩色图片具有三个通道,所谓的RGB图片,也就是在红色、绿色和蓝色三个颜色的矩阵,每个像素值都是[0,255]的值。灰度图片只有一个通道,所以只有一个矩阵。
卷积层
CNN由卷积而得名,那么什么是卷积呢?先来看图片
首先我们有如下的5*5的矩阵,它的每个像素值都由0或者1组成
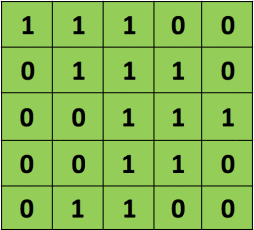
再来一张如下的3*3的矩阵
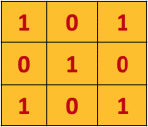
用这个33的矩阵对以上55的矩阵进行卷积,可以表示为如下的过程,
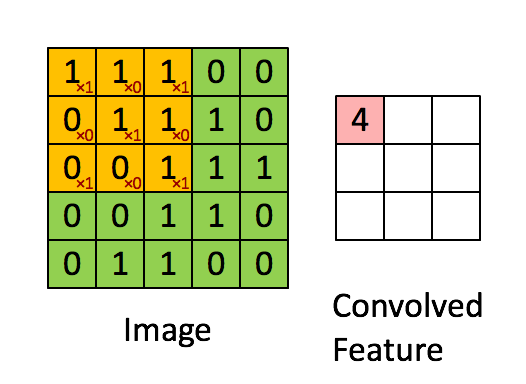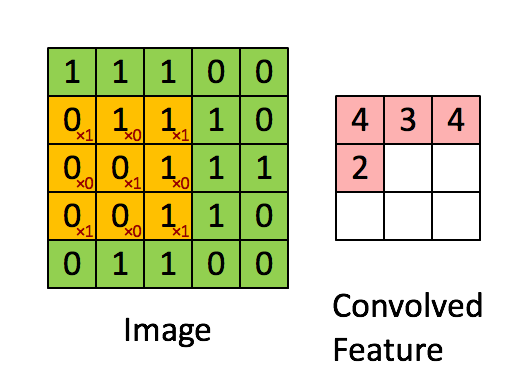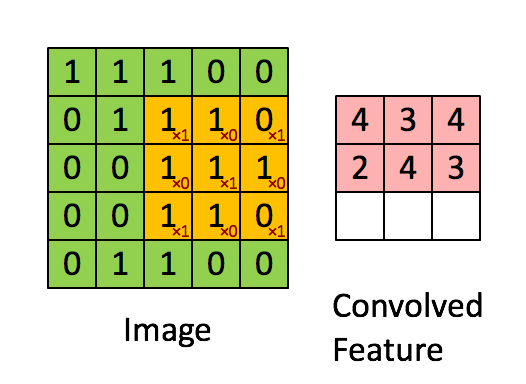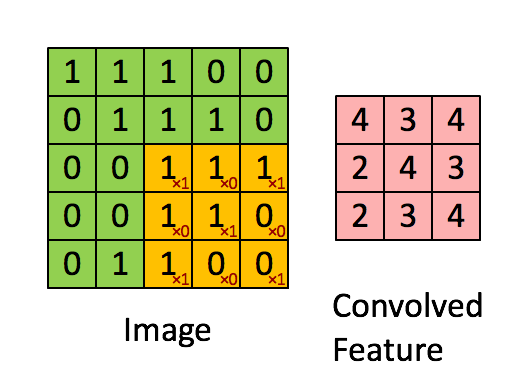
上述过程可以描述成,33的矩阵首先定位到55的矩阵的左上角,两者覆盖重叠到的部位进行点乘再求和,得到的值是新的矩阵的左上角第一个元素,接着33矩阵向右移动一个像素,也叫一个stride,进行下一次卷积操作,知道遍历完毕,得到一个新的矩阵。在CNN中,这个33的矩阵叫做滤波器或者卷积核,得到的新的矩阵叫做特征映射。可以说,卷积核的作用就是从原图片中发现特征。所以对于同一张图片,我们可以用不同的卷积核去操作,得到完全不同的特征映射。考虑如下的图片,

我们用不同的卷积核进行操作,得到的结果如下,

另一个例子如下,

如图,两个非常相似但是方向不同的卷积核对同一张图片进行卷积,得到的不同的结果。在训练过程中,CNN会自动学习到这些卷积核的参数,但是我们还有一些超参数需要手动确定,如卷积核个数、大小以及网络的结构等等。而特征映射的大小由三个参数来确定,
- Depth:也就是卷积核的个数,我们用几个卷积核进行操作,那么就可以得到多少个重叠着的特征映射,也就是特征映射的深度。
- Stride:卷积时每步移动的大小,容易得知,步子越大,那么卷积的次数也就越小,那么特征映射矩阵也就越小。
- Zero-Padding:指的是是否在原图像周围补上零再进行卷积,,这样也是控制特征映射大小的方法,带有Padding和不带有Padding的卷积分别叫做宽卷积和窄卷积。
非线性映射(ReLU)
ReLU函数是什么?初一看它的全称Rectified Linear Unit好像特别高大上,其实它的函数形式非常简单,就是
$$output = max(0, input)$$
也就是将原输入的负值全部替换为0。顺便一说,深度学习业界充斥着这种现象,如多层感知机与神经网络、甚至是Deep Learning这个称号本身都是这样改过来的“好名字”,不得不说,起个好名字对于成功也是非常主要的啊!
话说回来,用ReLU处理过的图片的效果如下:

除ReLU之外,还有sigmoid函数和tanh双曲函数等非线性变换,但是ReLU被证明表现更加,所以也就更常用。
池化层
池化(pooling)也就是信号处理领域的下采样Downsampling,其作用是对特征映射保留主要信息的同时进行降维。根据计算方式的不同可以有Max、Average、Sum等多种pooling方式。
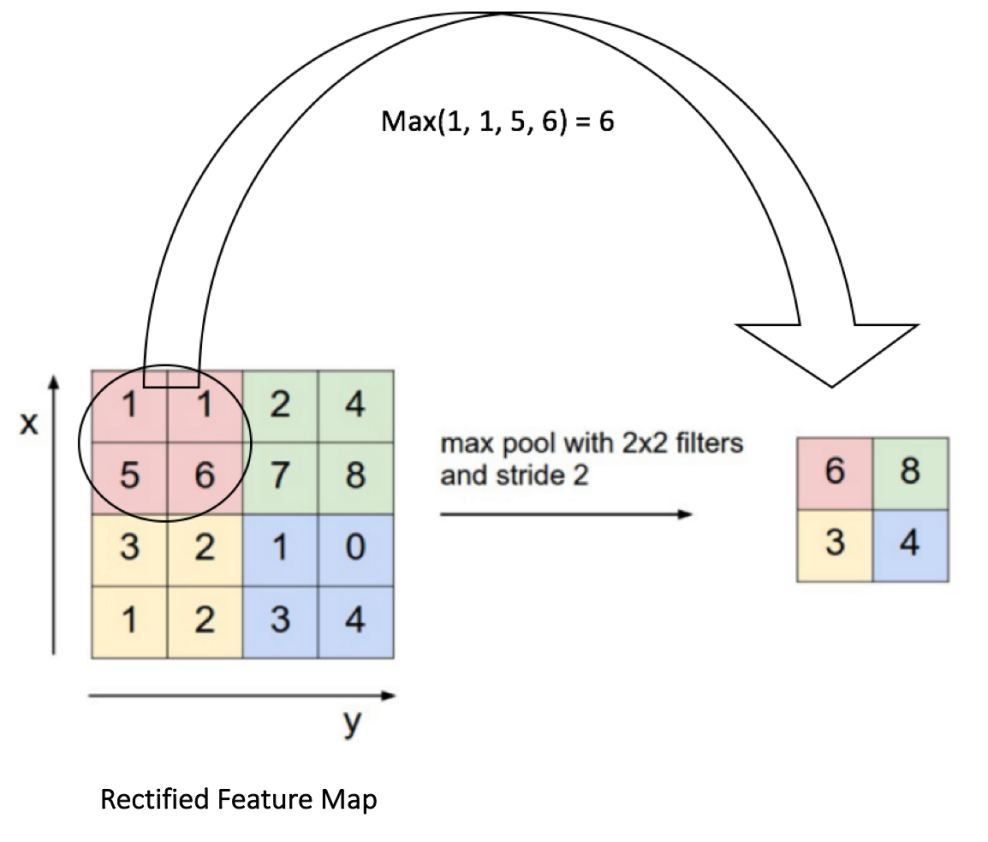
以上展示了使用2*2的窗口对经过卷积和非线性映射的矩阵的Max pooling操作。这里的stride是2个像素,对每个区域采用最大值。在网络中,pooling是对每个特征映射单独操作的,于是我们会得到相同数目的输出。
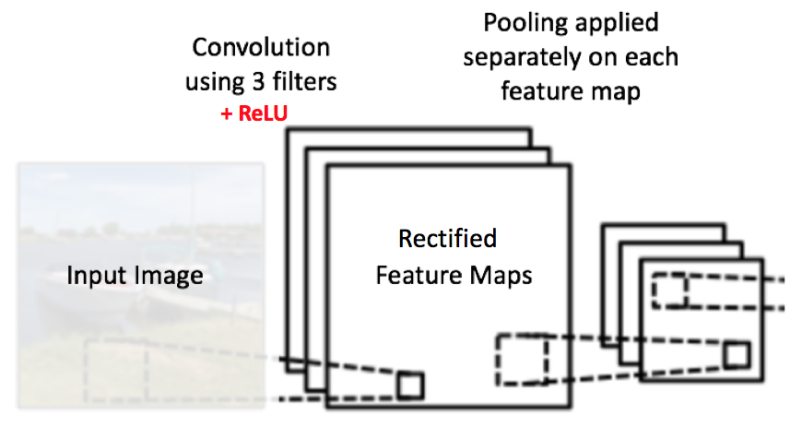
下图展示了pooling操作,
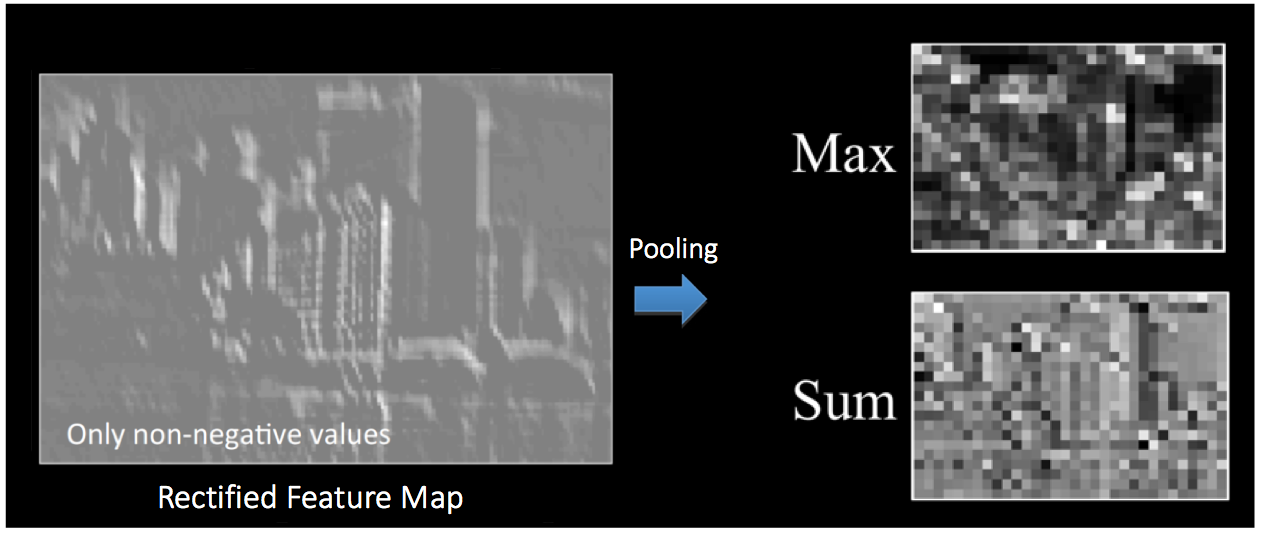
pooling操作显著地减小了输入的空间大小,除此之外,
- 使得输入更加小,更加容易计算
- 减小网络的复杂程度,有利于对抗过拟合
- 使得网络对于扰动等噪音更加鲁棒,因为微小的扰动对于pooling结果没有影响
- 有益于物体探测的准确性
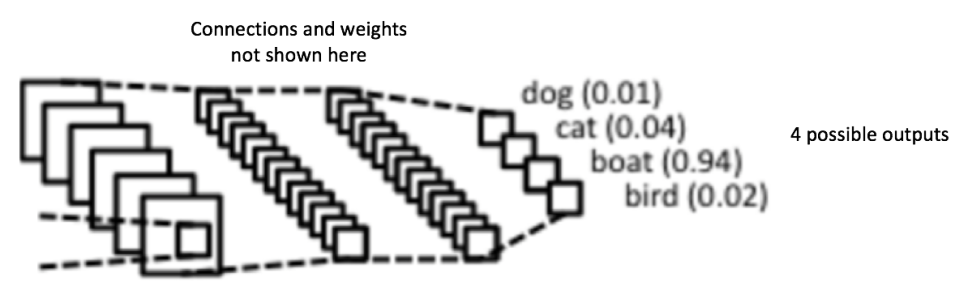
全连接层
经过两轮的卷积-ReLU-pooling操作,接下来就是标准的全连接神经网络结构了,所谓全连接,也就是上一层的每个神经元都与下一层的每个神经元有连接,倒数第二层的输出是每个类的概率,再经过一个softmax层进行归一化处理,我们得到了最终的输出:和为1的每个分类的概率。
训练过程
上面把CNN拆开了讲,接下来我们把各个组件合起来看一下CNN的训练过程。比如我们的输入是一张船的图片,而输出则是属于船的概率是1,如[0,0,1,0]。
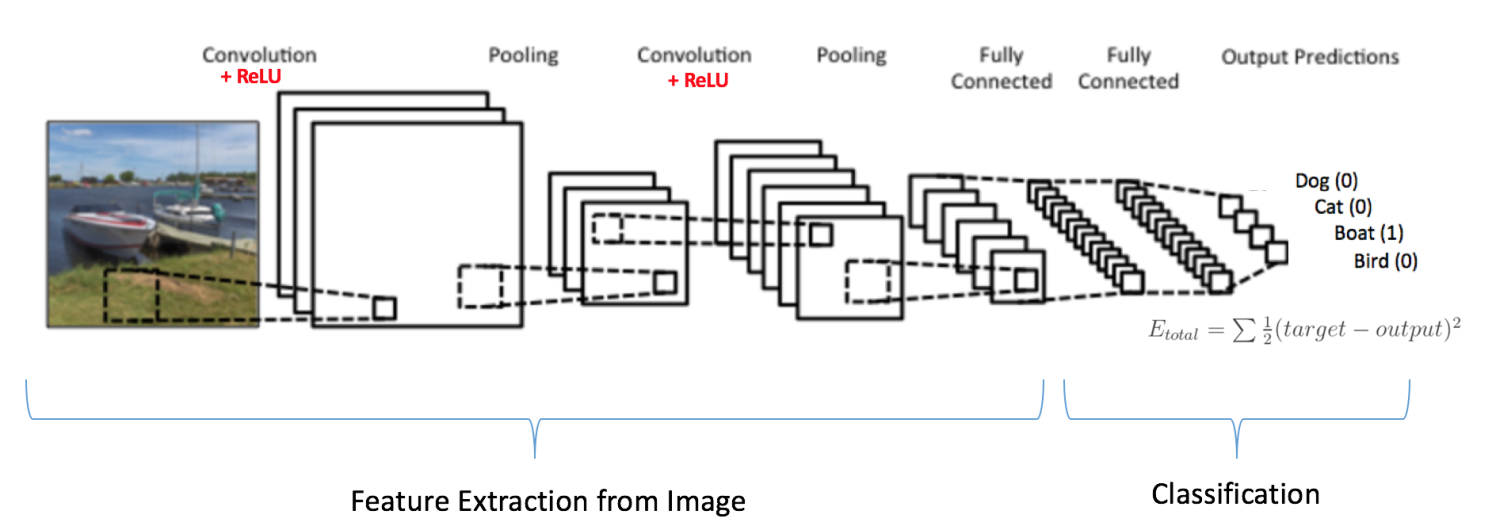
那么训练过程如下
- 步骤1:以随机值初始化卷积核和权重参数
- 步骤2:网络得到输入,进行前向的计算(卷积、ReLU和pooling)得到最终各分类的概率,假设是[0.1, 0.3, 0.2, 0.4],因为参数都是随机的,那么结果肯定也是随机的
- 步骤3:利用平方误差计算错误的损失函数大小
- 步骤4:反向传播计算error对于各个参数的梯度,对参数进行更新,以减小错误程度
- 注意到我们只更新卷积核的参数以及全连接的权重,其余的参数已经在训练之前指定
- 在训练过程中,网络逐渐“学习”到如何正确分类图片,这是通过逐渐修改更新参数得到的
- 步骤5:对于所有训练集内的图片重复步骤2-4
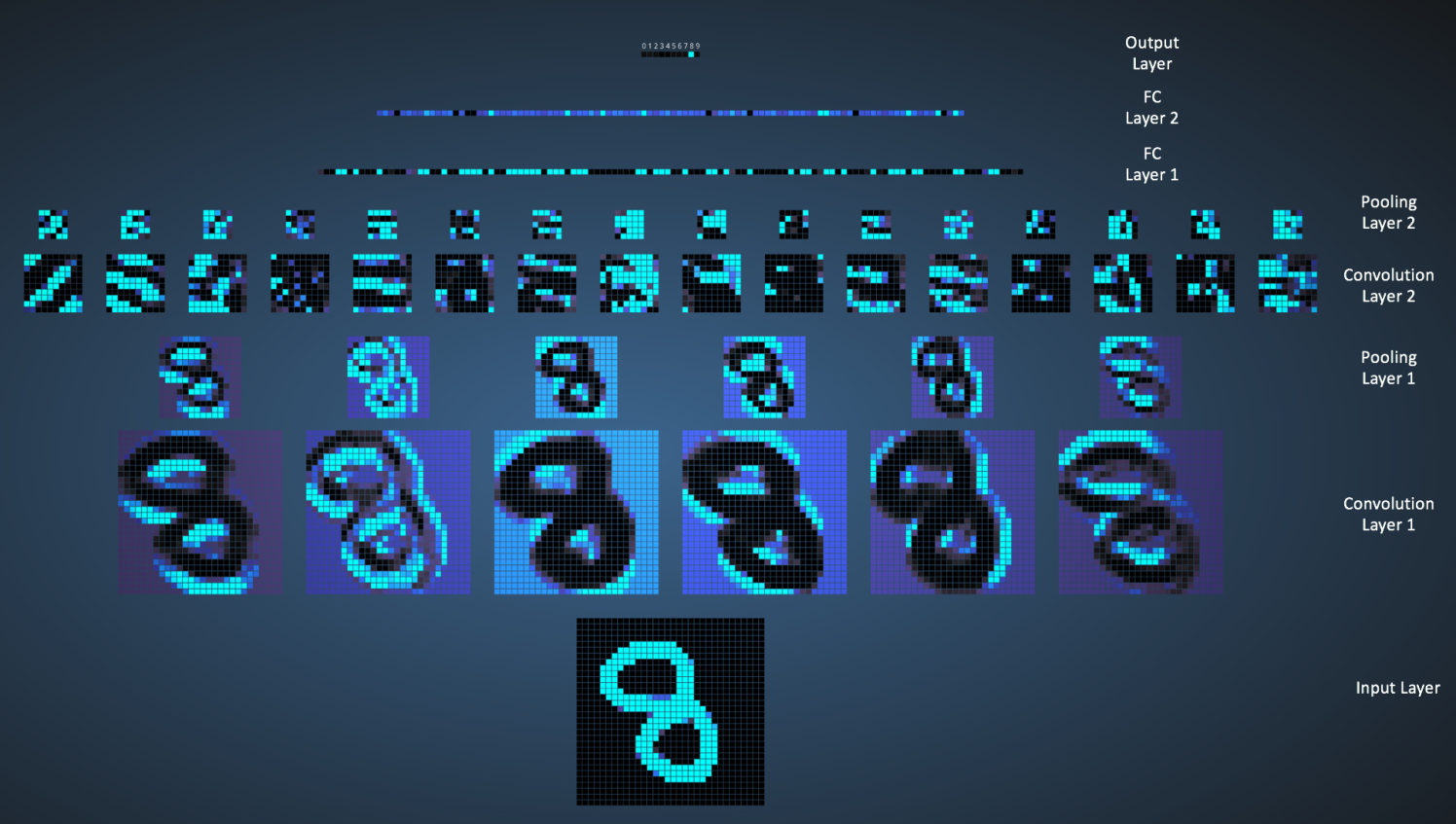
CNN的可视化
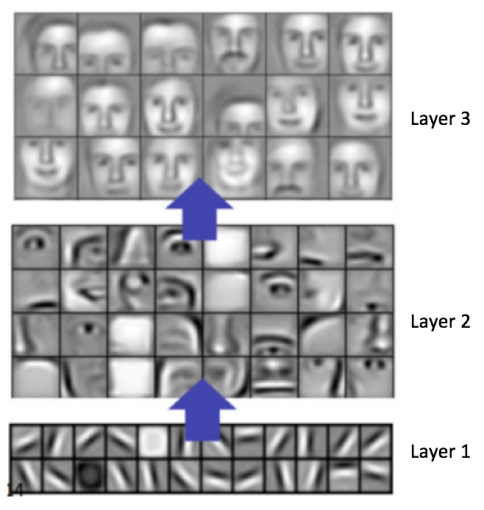
CNN在人脸识别内的应用,如上图所示。对于CNN的原理,结合上图我们可以进行如下的解释:CNN的卷积核由下到上是逐渐探测复杂的特征的,比如第一层卷积核的特征映射是简单的明暗线段纹理,第二层就可以得到曲线等复杂一些的特征,到了第三层探测的特征已经是人脸的形状轮廓了,后面的层对于前面层的特征进行组合变化而得到更加复杂的组合。这就类似单层感知机连异或函数都无法表示,多层感知机组合起来也就是神经网络却可以拟合任意复杂的函数的原理一样。
这里有一个很棒的关于CNN原理的展示demo,如图