tutorial

RECURRENT NEURAL NETWORKS TUTORIAL, PART 3 – BACKPROPAGATION THROUGH TIME AND VANISHING GRADIENTS

在之前的部分我们实现了RNN，但是并未深入探究时间反向传播算法，本文将对这一点作详细说明。我们将了解关于梯度消失问题的知识，它促使了LSTM和GRU的出现，而这两者都是NLP领域非常常见的模型。

##BACKPROPAGATION THROUGH TIME (BPTT)

首先我们回顾一下RNN的基本等式：

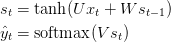
我们也定义了损失函数（交叉熵）：

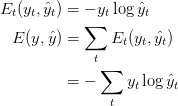
在这里，$$y_t$$是 $$t$$时刻的正确的词语， $$\tilde{y_t}$$ 是我们的预测。因为我们把一整个序列（句子）当做是输入，那么错误等同于每个时间step（词语）的错误的和。

![](/images/2016/06/rnn-bptt1.png）

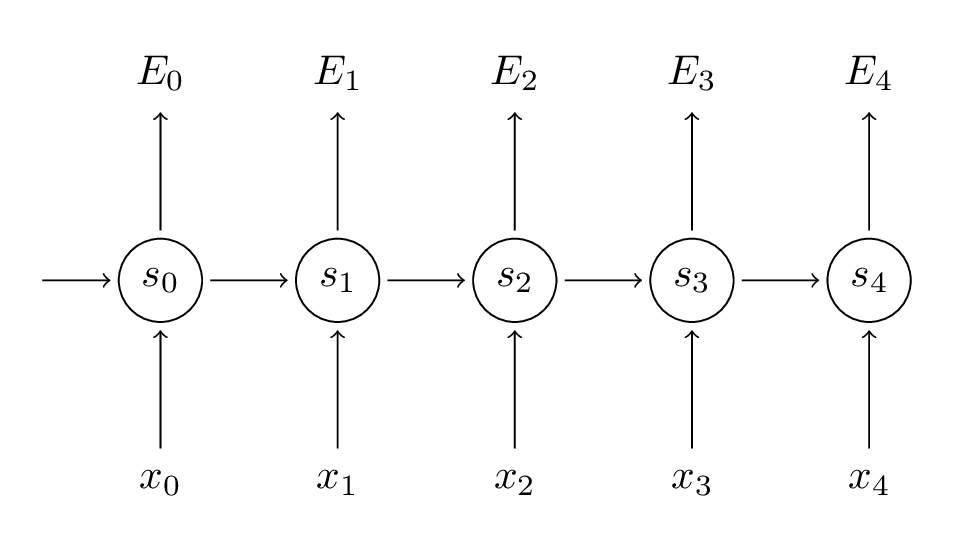
需要注意，我们的目标是计算基于参数$$U, V, W$$错误的梯度，并且通过SGD来学习到好的参数。类似于我们将错误相加的做法，对于一个训练样本，我们将各个时间点的梯度相加。

$$
\frac{\partial{E}}{\partial{W}} = \sum_{t} \frac{\partial{E_t}}{\partial{W}}
$$

我们使用链式求导法则来计算这些梯度，这就是反向传播算法:从错误处反向计算。以下我们使用$$E_3$$作为例子。

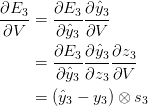
其中，$$z_3 = V s_3$$，并且$$\otimes$$指的是向量外积。在这里我们需要注意到，$$\frac{\partial{E_3}}{\partial{V}}$$只取决于当前时刻的值$$\tilde{y_3}, y_3, s_3$$。如果你明确了这一点，那么计算$$V$$的梯度只是矩阵计算罢了。

但是，对于$$\frac{\partial{E_3}}{\partial{W}}$$和$$V$$就不一样了。我们写出链式法则：

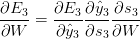
可以看到，$$s_3 = \tanh(U x_t + W s_2)$$取决于$$s_2$$，而$$s_2$$又取决于$$W$$和$$s_1$$，以此类推。所以我们计算$$W$$的偏导，我们不能把$$s_2$$当做一个常量，相反我们需要一遍遍的应用链式法则：

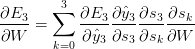
我们把每个时间点对于梯度贡献综合起来。换句话说，因为$$W$$在直到我们需要输出的时刻都被用到，所以我们需要计算$$t=3$$时刻直到$$t=0$$时刻：

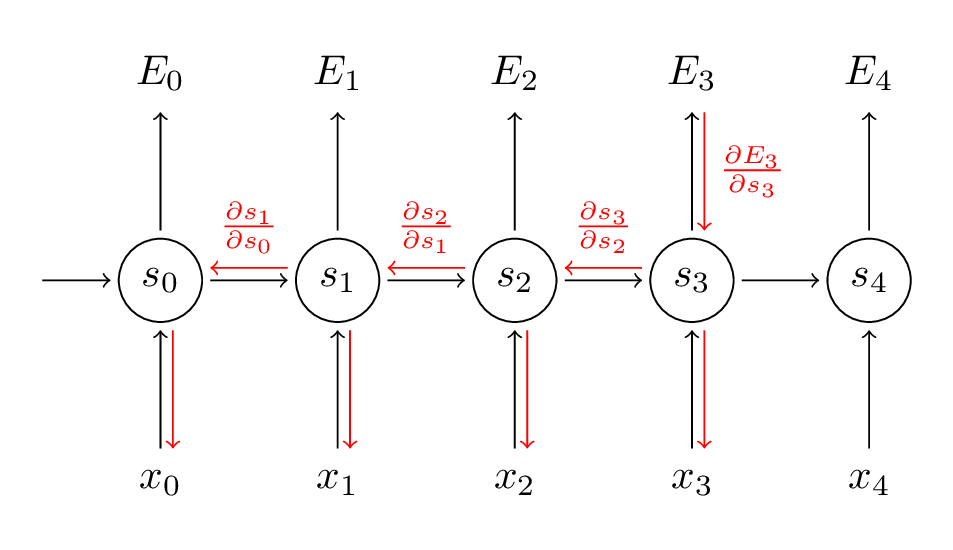
这其实和深度前馈神经网络里的标准的反向传播算法是类似的。主要的不同点在于我们把每个时间点的$$W$$的梯度综合起来。传统的神经网络的不同层之间不共享参数，于是我们也不需要综合什么。但是在我看来，BPTT只不过是在没有展开的RNN上的标准BP算法的别名罢了。类似于标准的BP算法，你也可以定义一个徳塔项来表示反向传播的内容。例如：$$\delta_{2}^{(3)} = \frac{\partial{E_3}}{\partial{z_2}} = \frac{\partial{E_3}}{\partial{s_3}} \frac{\partial{s_3}}{\partial{s_2}} \frac{\partial{s_2}}{\partial{z_2}}$$，其中$$z_2 = Ux_2 + Ws_1$$。以此类推。

代码实现BPTT如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def bptt(self, x, y):
    T = len(y)
    # Perform forward propagation
    o, s = self.forward_propagation(x)
    # We accumulate the gradients in these variables
    dLdU = np.zeros(self.U.shape)
    dLdV = np.zeros(self.V.shape)
    dLdW = np.zeros(self.W.shape)
    delta_o = o
    delta_o[np.arange(len(y)), y] -= 1.
    # For each output backwards...
    for t in np.arange(T)[::-1]:
        dLdV += np.outer(delta_o[t], s[t].T)
        # Initial delta calculation: dL/dz
        delta_t = self.V.T.dot(delta_o[t]) * (1 - (s[t] ** 2))
        # Backpropagation through time (for at most self.bptt_truncate steps)
        for bptt_step in np.arange(max(0, t-self.bptt_truncate), t+1)[::-1]:
            # print "Backpropagation step t=%d bptt step=%d " % (t, bptt_step)
            # Add to gradients at each previous step
            dLdW += np.outer(delta_t, s[bptt_step-1])
            dLdU[:,x[bptt_step]] += delta_t
            # Update delta for next step dL/dz at t-1
            delta_t = self.W.T.dot(delta_t) * (1 - s[bptt_step-1] ** 2)
    return [dLdU, dLdV, dLdW]

从代码你也可以观察到RNN不容易训练：由于序列比较长，每次传播需要计算很多层，实践上通常许多人的做法是将传播限制在几步之内。

##梯度消失问题

之前的部分我们已经讲述了关于RNN的长期依赖问题。为了解这一点，我们来观察上面我们计算过的梯度。

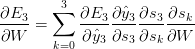
注意到是对于自身的链式法则，如。再注意到，我们这里计算的是向量对向量的偏导，其结果是一个雅可比矩阵。因此可以改写上面的梯度式为：

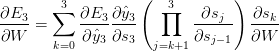
式子中的雅克比矩阵的二范数具有上限1.这导致激活函数tanh（或者sigmoid）映射所有的值到[-1,1]，那么偏导也被限制在1（对于sigmoid是$$\frac{1}{4} $$）。

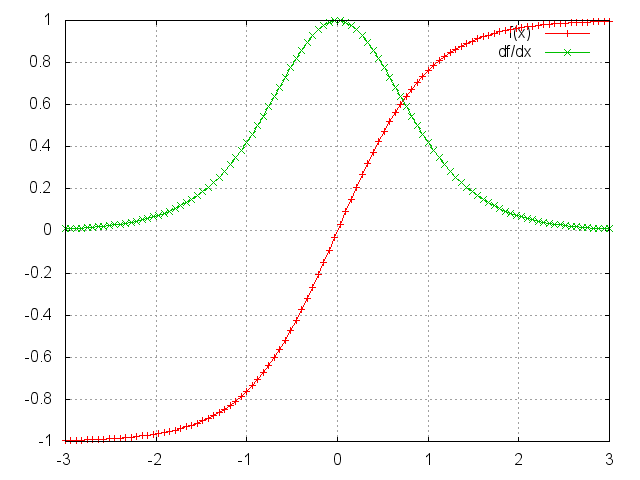
图中我们可以看到，在tanh函数两边，梯度都接近于0.这导致它之前的梯度也接近于0，那么，与矩阵中的数字多次相乘使得梯度迅速减小，直到接近消失。院出的时间点对于现在的影响接近于0，这就是长期依赖问题的原因。但是，长期依赖问题并不只是对于RNN出现，深度神经网络都具有这个问题，只不过RNN经常要处理长序列问题，所以网络层数很多，这个问题就经常出现了。

容易想到的是，与梯度消失问题对应的是，梯度爆炸问题。当雅克比矩阵中的数值较大时，容易出现这个问题。但是，通常来说，对于梯度爆炸，业界关注并不太多。有两个原因，其一，梯度爆炸发生时通常容易发现，因为可能导致程序崩溃之类的后果；其二，通常为梯度设置上限是应对梯度爆炸的简便做法。

那么怎么应对梯度弥散问题呢？首先，更好的初始化权重可以减少梯度弥散的效果；其次，使用正则化；更加通用的方法是使用ReLU作为激活函数，其梯度要么是1要么是0，所以更少的可能出现梯度弥散的问题。另外，更加流行的做法则是使用 Long Short-Term Memory (LSTM)或者Gated Recurrent Unit (GRU)，LSTM出现于1997年，也许是NLP领域近期最流行的网络结构。GRU，出现于2014年，是LSTM的简化版本。两种网络都是为了应对梯度弥散和长期依赖问题。我们将会在之后的教程中涉及它们。