本文中,我们将学习关于LSTM (Long Short Term Memory)网络和 GRUs (Gated Recurrent Units)的知识。LSTM最初由Sepp Hochreiter and Jürgen Schmidhuber于1997年提出,如今是深度学习自然语言处理领域最流行的模型。GRU,出现于2014年,是LSTM的简化版,与LSTM有许多相似的特性。
##LSTM 网络
在第三部分我们提到了梯度消失问题妨碍了标准的RNN学习长期依赖问题。LSTM被设计于用gate结构解决梯度消失问题。为了理解这个机制,我们来看看LSTM如何计算隐藏状态$$s_t$$(其中小圆圈代表Hadamard product,即同型矩阵各元素对应相乘,不同于矩阵点乘)。
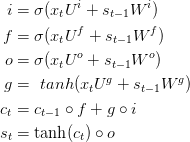
式子看起来复杂,一步一步来理解实则简单。首先,LSTM的一层代表的只是另一种计算隐藏层的方法。之前我们计算了隐藏状态$$s_t = tanh(Ux_t + WS_{s-1})$$。对于当前的单元,输入是$$t$$时刻的$$x_t$$,而$$s_{t-1}$$是之前的隐藏状态,输出是新的隐藏状态$$s_t$$。其实,LSTM做的事情是完全一样的,只不过换了种方式,这也是理解LSTM的核心。我们可以把LSTM单元看作是黑盒子,给予其当前输入和之前的隐藏状态,它可以输出下一个隐藏状态。
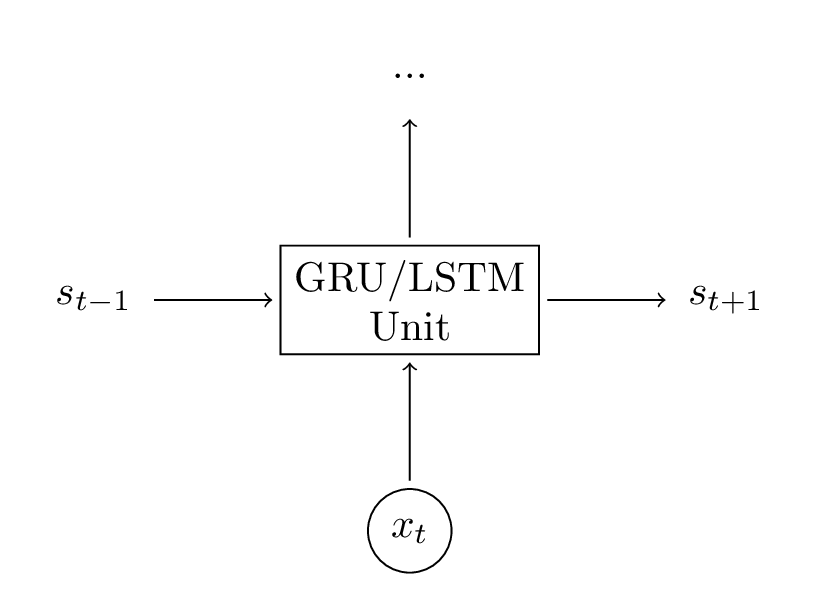
把这个牢记于心,我们开始来阐述LSTM如何计算隐藏状态。关于这一点,详细可看这篇文章,这里我们只作简短描述:
- $$i,f,o$$分别被称为输入门、遗忘门和输出门。注意到,它们具有相同的等式,只是参数矩阵不同。它们之所以被称为“门”,是因为sigmoid函数将向量值压缩到0和1之间,再与另一个向量相乘,我们因此决定向量的多少“通过”。输入门决定当前输入计算出来的状态的多少成分被通过,遗忘门决定之前的状态有多少可以被保留到之后,输出门决定当前的状态有多少被传送到外层的网络(高层网络和下一时刻)。这些门的维度都是$$d_s$$,即隐藏层的大小。
- $$g$$是一个候选的隐藏状态,基于当前的输入和之前的隐藏状态计算而出。其与vanilla RNN的计算等式相同,只是把参数$$U,W$$改名为$$U^g,W^g$$。和RNN的直接将$$g$$作为心的隐藏状态不同,我们将其通过一个输入门来决定保留它的多少成分。
- $$c_t$$是单元的内部的记忆,它由之前的记忆$$c_{t-1}$$通过遗忘门再加上新计算出来的隐藏状态$$g$$通过输入门计算得出。因此,它代表了旧的记忆与新的输入的结合。我们可以选择全部忽略旧的记忆(遗忘门全部置零),或者忽略全部的计算出的新状态(输入门全部置零),但是通常来说,我们可能更希望介于两者之间。
- 给定记忆$$c_t$$,我们最终通过让记忆和输出门相乘计算出输出隐藏层状态$$s_t$$。在网络内,不是所有的内部记忆都与其他单元使用的隐藏状态有关。
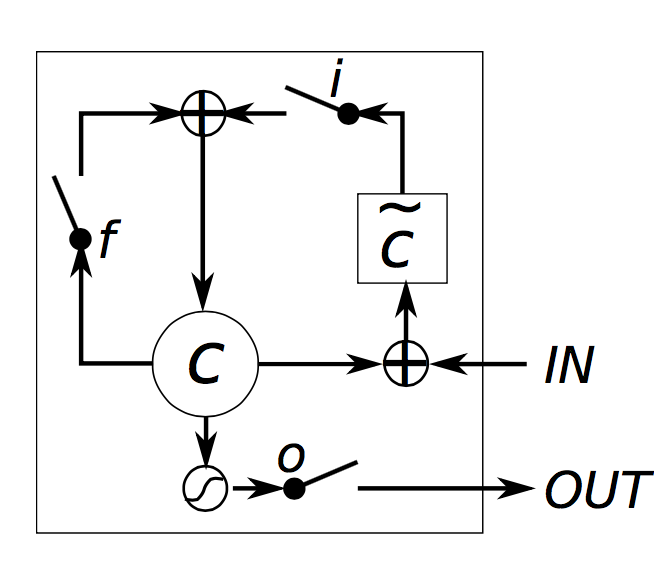
换一种说法,我们可以将标准的RNN看作是特殊的LSTM,如果我们将遗忘门全部置零,输入门全部置一,输出门全部置一,我们就几乎得到一个标准的RNN。通过门机制,LSTM可以操作记忆从而解决长期依赖问题。
注意到,还有许多的LSTM变种,一种添加上“猫眼”结构,它的门同时取决于之前的隐藏状态$$s_{t-1}$$和之前的内部状态$$c_{t-1}$$。 LSTM: A Search Space Odyssey 实验观察了许多不同的LSTM机制。
##GRU网络
GRU的理念类似于LSTM,其等式如下:
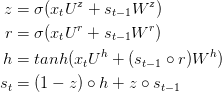
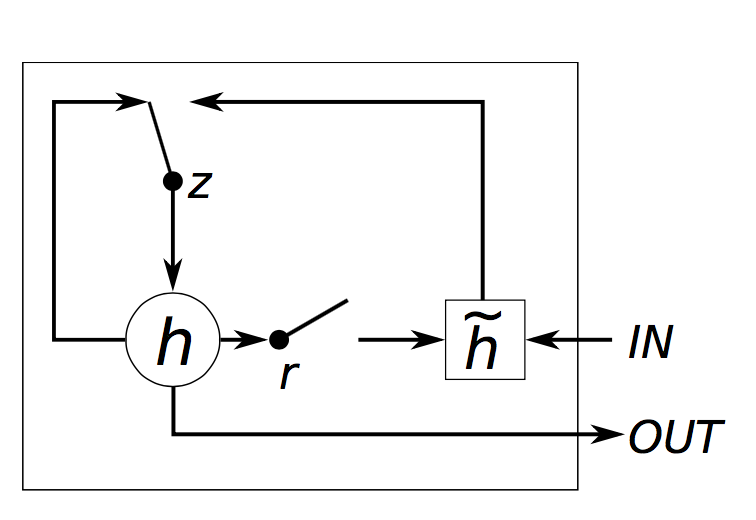
GRU拥有两个门,称为重置门$$r$$和更新门$$z$$。直观来说,重置门决定如何联合新的输入和之前的记忆,而更新门决定留下多少之前的记忆。如果将重置门全部置一并且更新门全部置零,那么我们又得到了我们原始的RNN了。GRU的解决长期依赖的理念和LSTM基本类似,以下是一些不同之处:
- 两个门VS三个门
- GRU不处理内层记忆$$c_t$$
- 输入门和遗忘门被组合成更新门$$z$$,重置门$$r$$直接连接之前的隐藏状态。因此,
- 计算输出是不加上第二个非线性变换
##GRU VS LSTM
如今你认识了两个对抗梯度消失的模型